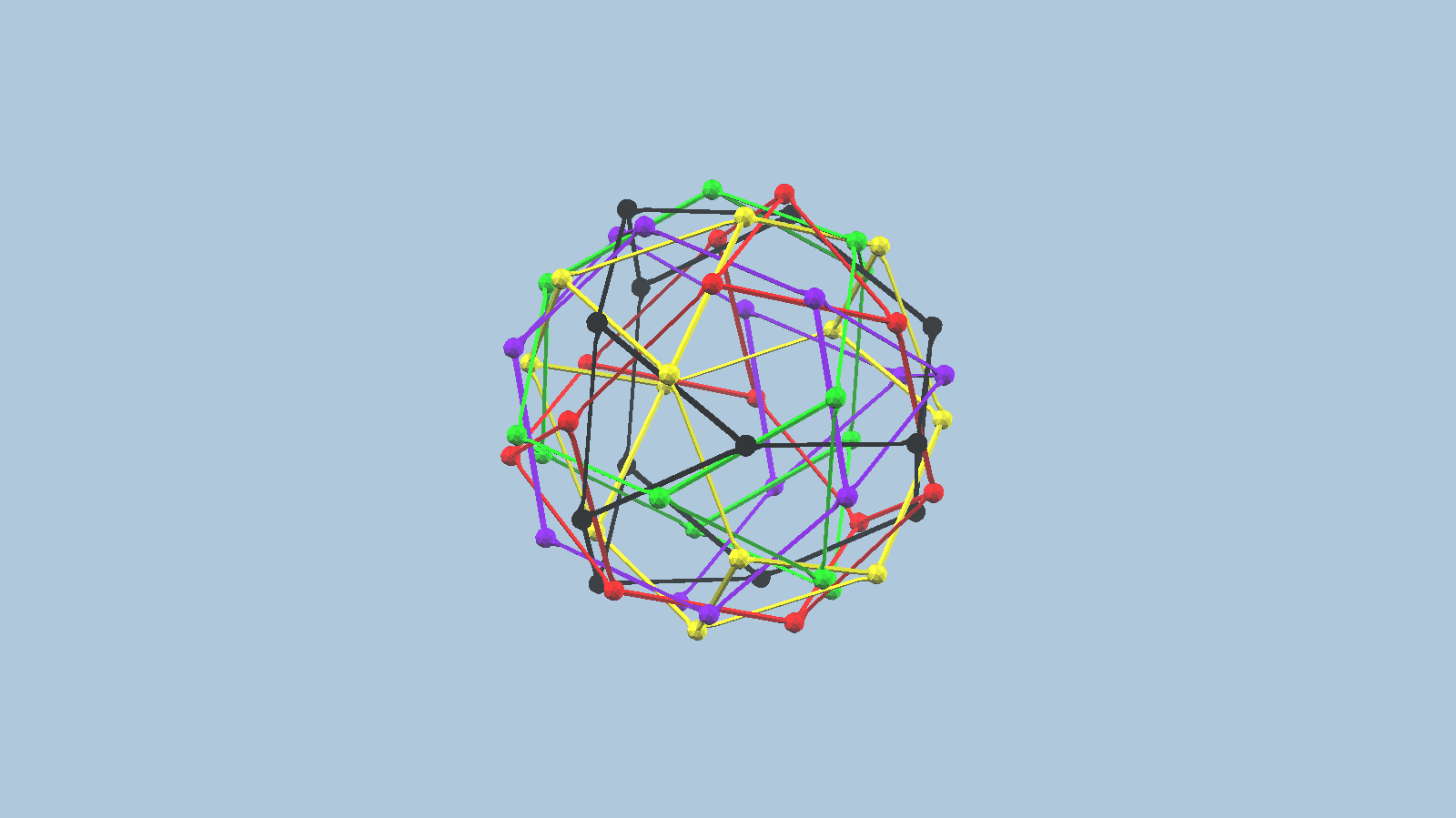
A model proposed by George Hart more than 20 years ago.
Firstly, build a regular tetrahedron with edge length 3g2. Attach parallel pentagons with edge length 3b1 at both vertices of a single edge. These pentagons will serve as a support structure. Then build the other 4 tetrahedra, one at a time. No dexterity is needed. The more tetrahedra are already present, the more attention is needed to correctly weave new edges in between existing ones. It helped me a lot to use coloured Zome balls, precisely as in the vZome model.
Finally, introduce 60 g2 edges to construct the truncation of all tetrahedra, remove the b1 struts of both supporting pentagons, and remove the vertices and corresponding g2 struts of all tetrahedra.
The five truncated tetrahedra, not connected to each other via Zome connectors, will not lock each other in place, unless build at this scale.